SAST (Static Application Security Testing) — метод тестирования защищенности приложений, который анализирует их исходный код и компоненты с помощью разных подходов, алгоритмов и технологий. Среди них есть символьное выполнение, с подробным описанием которого можно познакомиться здесь:
- Symbolic Execution. 17-355/17-665/17-819O: Program Analysis (Spring 2018);
- Ищем уязвимости в коде: теория, практика и перспективы SAST.
Говоря простым языком, этот подход строится на следующих постулатах:
- При анализе исходный код преобразуется в другое представление для сбора необходимых свойств, при этом явная интерпретация кода не производится.
- Все входные данные (аргументы функций точек входа, обращение к файловой системе, внешним сервисам и т. д.) считаются неизвестными и помечаются как символьные значения, которые могут принимать любые доступные значения, пока на них не наложены ограничительные условия.
- Учитываются все возможные пути разветвления исходного кода, соответствующие языковым конструкциям ветвления управления, где ветвление может достигаться в том числе за счет символьных неизвестных значений.
Для простоты понимания будем использовать следующие термины:
- Вариантом будем называть пару
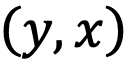, где 
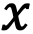— некое значение, а 
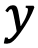— условие достижимости этого значения. Обозначать будем как 
- Вариативным множеством будем называть множество всех вариантов выражения. Обозначать будем как
.
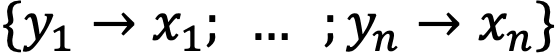Фундаментальная проблема подхода
В прошлых статьях (1, 2) мы уже говорили о том, что символьный анализ имеет экспоненциальную сложность, и рассматривали различные подходы к решению этой проблемы. Если коротко, то
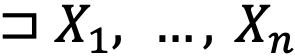— вариативные множества: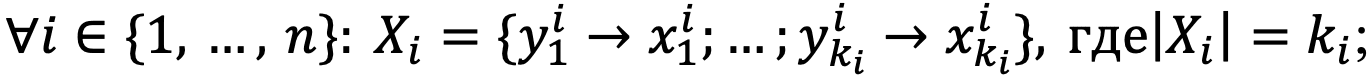 
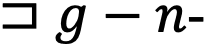мерная функция языка (сложение, конъюнкция и др.), в частности, определено 
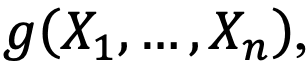тогда количество вариантов выражения 
равно:
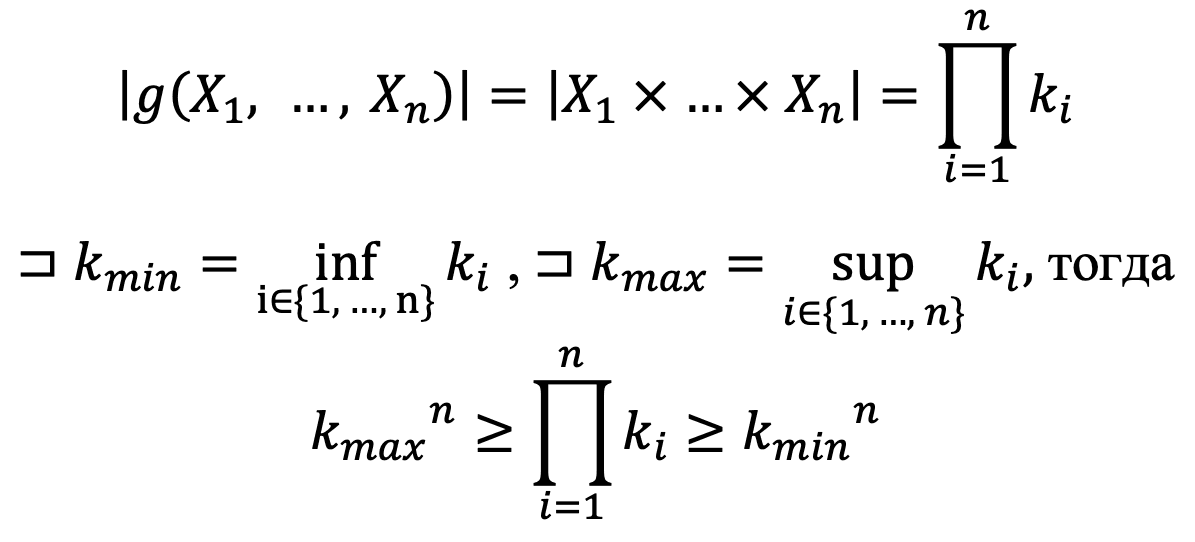
Откуда и следует показательная (грубо говоря, экспоненциальная) скорость роста данных.
Если посмотреть на представление некоторого выражения 
с подвыражениями (из прошлых статей) относительно символьных неизвестных и содержащихся в нем вариативных множеств (см. рис. 1), то станет понятно, что количество вариантов всего выражения ощутимо быстрее растет по условиям вариантов вариативных множеств, нежели по значениям этих же вариантов.
Происходит это потому, что для каждого значения варианта в каждом вариативном множестве существует множество допустимых значений условия варианта. Из этого следует, что одному конкретному значению соответствует множество условий, приводящих к нему. Поэтому далее будут рассмотрены способы уменьшения и сдерживания множества достижимых условий выражений.
Хранение условий
Прежде всего необходимо понять, каким образом хранить условия, когда они состоят из каких-то конъюнктов и дизъюнктов, например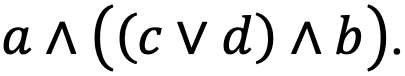 
Так как мы работаем с исходным кодом, все выражения могут быть транслированы в разные представления, одно из которых — AST — является абстрактным синтаксическим деревом. Значит, пример логического условия выше можно представить в этом виде следующим образом:
Формально такое представление будет описываться следующим образом: 
То есть дерево может быть либо терминальным (листовым) узлом с некоторым символьным выражением, либо нетерминальным — с типом операции и с правым и/или левым поддеревьями. Однако у такого способа хранения есть ощутимый недостаток — скорость поиска элементов, которая может быть линейно зависима от количества элементов, как показано на рис. 3.
Чтобы устранить эту проблему, сделаем следующие шаги. Во-первых, поэтапно изменим описание дерева:
То есть каждому узлу в бинарном дереве добавим числовой показатель — ключ, который соответствует символьному выражению в этом узле. Также в нетерминальных узлах заменим операцию на символьное выражение, при этом замененную операцию свяжем с самим деревом. Таким образом получим, что дерево может содержать только операнды одного типа операций в противовес тому, что было ранее. От ключа будем требовать только одно свойство: значения ключей для двух равных выражений должны быть равны, то есть если ключи разные, то и выражения будут неравными.
Во-вторых, будем использовать самобалансирующееся дерево поиска, сбалансированное по высоте: например, AVL, Reb-black tree, B-tree и др. Полное отличие сбалансированных по высоте деревьев от несбалансированных см. здесь, а если кратко, то оба типа деревьев балансируют свою высоту при различных операциях с ними. Но деревья первого типа гарантируют, что высота дерева не будет превышать некоторого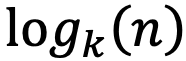 
(где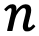 
— количество узлов в дереве, а 
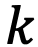— количество дочерних элементов нетерминальных узлов), тогда как деревья второго типа, несмотря на балансировку высоты, все еще могут иметь высоту, близкую к линейной .
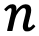Эти два шага позволят нам оптимальнее искать необходимые элементы. В качестве альтернативы можно рассмотреть хеш-таблицу (см. рис. 4), где для каждого выражения вычисляется хеш-значение по функции и определяется его место в таблице. Время поиска в таблице будет сопоставимо с полученным деревом с учетом того, каким образом решается проблема коллизий: через открытую адресацию, списки и др.
Способы сокращения
Далее рассмотрим простые подходы, которые можно применить для сокращения и сдерживания условий.
Первый — использование полиадических операторов, которые могут иметь любое количество операндов (по-другому их еще называют мультиарными или вариативными). Это позволит перейти от использования множества бинарных операторов к одному полиадическому оператору: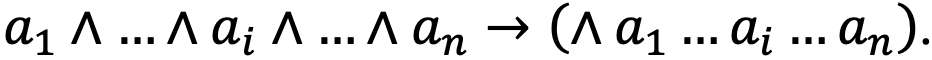 
В дальнейшем мы будем использовать соответствующую запись полиадических операторов.
Второй подход — использование свойств самой булевой алгебры, в которой находятся условия:
- идемпотентность:
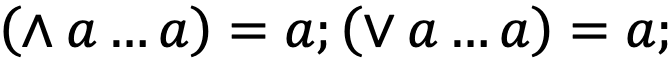
- поглощение:
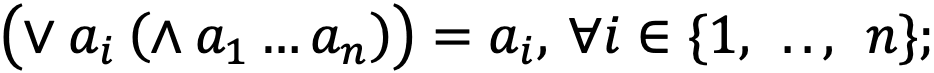
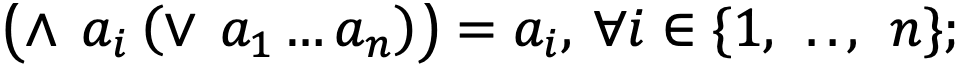
- Sup и Inf:
- коммутативность:
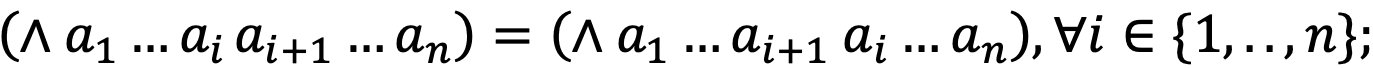
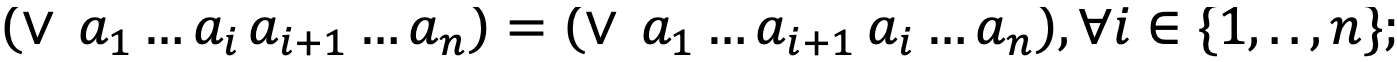
- ассоциативность:
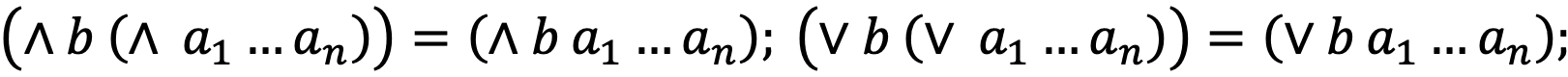
- дистрибутивность:
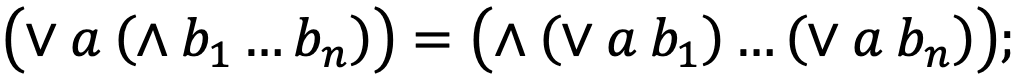
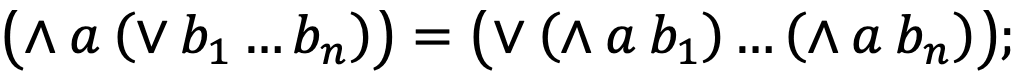
- инволютивность:
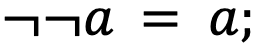
- дополнительность:
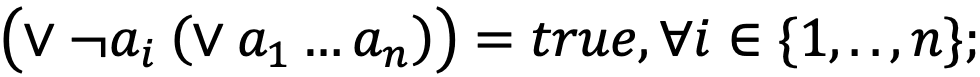
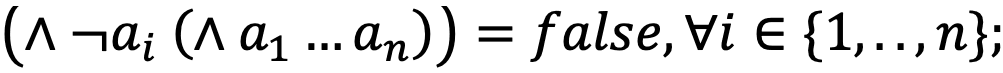
- законы де Моргана:
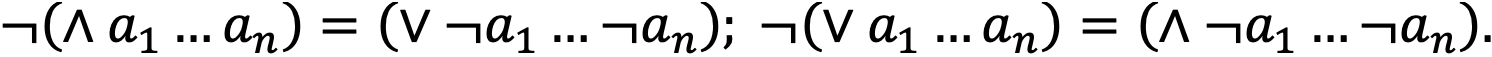
Это поможет нам экономить ресурсы, видоизменять и отбрасывать недостижимые условия и даже фиксировать единственный вариант с достижимым условием в вариативном множестве, что позволит ускорить время обработки данных при анализе. Однако на текущий момент есть один нюанс. Структура данных, которую мы рассматривали ранее, была заточена на быстрое нахождение элемента в ней. Но свойства булевой алгебры также требуют понимания, а имеется ли в ней элемент, противоположный текущему. Следовательно, для применения всех свойств необходимо будет делать два поиска в структуре — самого элемента и его отрицания, что не очень приятно.
Независимо от того, какую структуру данных рассматривать — полученное дерево или хеш-таблицу, поиск элементов в них происходит по определенному числу: числовому ключу или значению хеш-функции. Затем идет сравнение искомого элемента с предполагаемым равным в структуре данных. Сделаем структуру данных инвариативной относительно операции отрицания, то есть она будет считать, что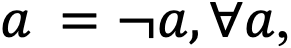 
соответственно, числовые показатели также будут считаться равными. Получается, что вместо двух операций поиска элемента и его отрицания со сравнениями будут выполнены одна операция поиска и две операции сравнения — чтобы определить, нашелся ли сам элемент или его отрицания. Это позволит использовать все свойства булевой алгебры оптимальнее.
Третий подход — использование нормальных форм представления логических условий. Конъюнктивная нормальная форма (КНФ) — булева формула, которая представлена в виде конъюнкций дизъюнктов литералов. Проще говоря, это конъюнкция, операнды которой не содержат других конъюнкций и содержат либо дизъюнкции, либо атомарную формулу, либо ее отрицание: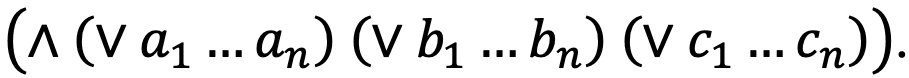 
Аналогично дизъюнктивная нормальная форма (ДНФ) — булева формула, которая представлена в виде дизъюнкции конъюнктов литералов: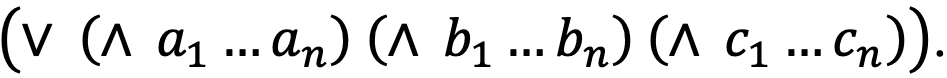 
Любую булеву формулу можно привести к одной из указанных выше нормальных форм. Для этого в нашем случае можно применить, по необходимости, следующие свойства булевой алгебры: законы де Моргана, инволютивность, дистрибутивность, дополнительность и поглощение, идемпотентность. Нормальные формы позволят держать все логические формулы в схожем виде, что упростит работу с ними — в частности, применение булевых свойств.
SMT
К текущему моменту мог возникнуть закономерный вопрос: зачем нужны все эти действия с условиями, если можно использовать различные SMT-решатели, которые покажут, выводима ли логическая формула и при каких значениях? Прежде, чем ответить на этот вопрос, замечу, что Satisfiability Modulo Theory (SMT) — это задача выполнимости в теориях, где задачей является определенная логическая формула, состоящая из утверждений относительно некоторой теории: целых чисел, векторов, строк и др. Выражение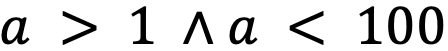 
является формулой над теорией целых чисел, а может быть и над теорией вещественных чисел: так как дополнительных ограничений больше нет, могут подходить сразу несколько теорий.
Соответственно, SMT-решатели решают задачу выводимости и говорят о достижимости или ее отсутствии, используя для этого синтаксис в терминах SMT, как показано в примере ниже.
(set-option :print-success false)
(set-option :produce-models true)
(set-logic QF_LIA)
(declare-const x Int)
(declare-const y Int)
(assert (= (+ x (* 2 y)) 20))
(assert (= (- x y) 2))
(check-sat)
; sat
(get-value (x y))
; ((x 8) (y 6))
Сначала устанавливаются опции для запроса, затем задается та логика (теория), относительно которой будут подаваться на вход логические формулы. После идет объявление переменных для запроса, следом задаются основные логические формулы и ограничения, требующие проверки выводимости. Под конец проверяется выводимость всего запроса. В случае выводимости запроса есть возможность получить конкретное множество значений переменных, приводящее весь запрос в достижимое состояние.
Теперь, когда мы кратко рассмотрели SMT, можно дать ответ на изначальный вопрос: зачем нужны все эти действия с условиями, когда есть SMT-решатели? Причина проста: далеко не всегда SMT-решатели способны решить логическую формулу за приемлемое время.
Рассмотрим пример: CVC5 v1.2 с опциями запуска -L smt2.6 --output-lang smt2.6 --incremental --produce-models --strings-exp на машине с Intel(R) Core(TM) i7-12700H 2.30GHz 14 Cores 64GB DDR5 4800 MHz.
(set-logic ALL)
(declare-const x Int)
(assert (= 1 (mod 0 (str.len (str.from_int (ite (= x 0) 0 (div 0 x)))))))
(check-sat)
В таких условиях решение не находится за десятки минут. Если взглянуть на инструкцию
(ite (= x 0) 0 (div 0 x)), то можно заметить, что она всегда возвращает 0. А при замене этой инструкции на явный 0 CVC5 начинает решать это выражение за считанные секунды.
Другой пример: z3 v4.14 с опциями запуска -smt2 -model -st -in на той же машине. Возьмем следующий запрос:
(set-logic ALL)
(declare-const id1 String)
(assert (str.contains (str.replace id1 “<” (str.replcae id1 “>” “”)) “<body>text</body>”))
(check-sat)
Он тоже не решается за десятки минут.
Третий пример: Yices2 v6.5 с опциями запуска --stats –interactive на той же машине
(set-logic QF_LIA)
(declare-const a Int)
(declare-const b Int)
(assert (not (and (≤ (mod b (-968)) (mod b 53)) (= (mod a 533) (- a b)))))
(assert (not (and (≤ (div b 432) (div a 492)) (< (- b b) (mod b (-554))))))
(assert (< b a))
(check-sat)
Запрос аналогично не решается за десятки минут.
Все потому, что задача SMT принадлежит классу NP-трудных задач: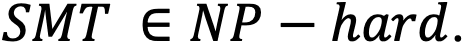 
То есть нет гарантий того, что разрешимость утверждений относительно выбранных теорий будет определена за полиномиальное время от недетерминированной машины Тьюринга и что она не потребует большего количества ресурсов. Например, для булевой теории разрешимость действительно достигается за полиномиальное время работы недетерминированной машины Тьюринга, но не во всех теориях присутствует такая же разрешимость. Даже если взять за приближение полиномиальное время на такой машине, это нереалистичное условия…
***
Мы рассмотрели далеко не все способы представления и использования логических формул, а также условий достижимости, но уже можно понять: если есть возможность применять различные хитрости для логических формул, это стоит делать. Таким образом можно сократить использование ресурсов в самых разных сферах: от выполнения программ с условиями до оптимизации запросов в базы данных. А в случае анализа кода это ускорит процесс, ведь SMT в общем случае может требовать много времени.
